




Teach Bike Riding In 2 To 10 Minutes
Fastest, easiest, safest, greenest patented teaching process with scientific certainty

The nature of bicycle balancing is such that virtually anyone can be taught to ride in just a few minutes.
The dominant force involved in bicycle balancing is centripetal force. High school physics text books usually cover circular motion and centripetal force as shown in the diagram below.
The key to understanding normal bicycle balancing is a little reverse thinking, which is what triggered the development of the Pedal Magic process.
Physics of bicycle balancing can be harnessed in minutes
Physics books discuss centripetal force in terms of the required amount of force towards the center of a circle to keep an object from veering off its circular path.
Normal bicycle balancing is related to centripetal force
Applying this principle to bike riding, physics books would say that a bicyclist has to tilt the bike X degrees off the vertical towards the center of the circle to create sufficient centripetal force to remain on the circle. This is usually discussed within the context of a bicyclist negotiating a curve on a path.
Value of X (how much to tilt or lean) is calculable from equation inside the circle (m is mass of bike and rider, g is acceleration due to gravity, v is the velocity of the bike, and R is radius of the circle).
If X is too large (i.e. rider tilts too much into the circle), centripetal force will be too much and the bike will start turning into a circle with radius smaller than R. If X is not large enough, there won't be sufficient force to keep the bike on the circle and the bike will veer off, turning in a circle with radius larger than R.
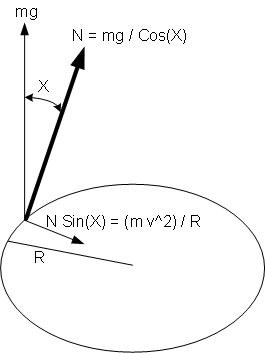
What we are interested in is not what the value of X should be to keep a bike on the circle, but what we should do to reduce the value of X (i.e. reduce the tilt to bring the bicycle into upright position).
Balance equation in the circle tells us that to reduce X, the rider needs to create an opposite force larger than the existing value of the right hand side of the equation. This can be done by increasing v (velocity) in the numerator, reducing R (radius) in the denominator, or doing both.
Counteracting centripetal force to keep bicycle in balance
From the balance equation we can deduce that if R is not reduced quickly enough X will increase immediately, resulting in a crash. We can also deduce that if R is always reduced enough immediately as the bike tilts from one side to the other, the bike will not crash. It is easily observed that when a rider is pedaling at a constant speed s/he keeps the bicycle in balance by continuously creating counteracting forces subtly with the handlebar as the brain senses in the background that the bike is starting to lean to one side or the other.
Inevitability of crashing as well as staying in balance
Physics Of Bicycle Balancing
“The only certain barrier to truth is the presumption that you already have it.” -